2023年11月27日,北京应用物理与计算数学研究所苗长兴教授,应邀为数学科学学院师生做了题为“调和分析内涵、思想及其派生方法”的学术报告。报告由张安老师主持。
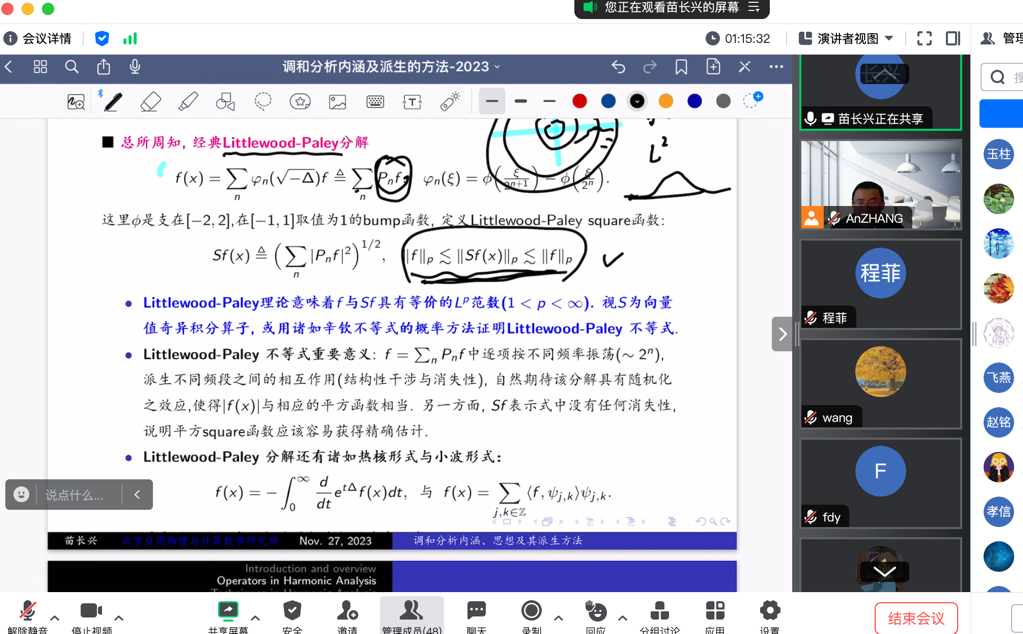
本次报告,苗老师从不同角度和新的视角介绍了调和分析思想的精髓,特别是同其他不同学科之间的紧密联系。现代调和分析对应着相空间上的分析, Heisenberg原理是沟通物理空间与频率空间的桥梁, 从微分算子、拟微分算子、Fourier积分算子的发展过程充分体现了现代调和分析研究对象的转变及几何融入分析的自然性(相空间上调和分析对应着余切丛上的分析).“分而治之”是调和分析技术的主要特征, “艺术与哲学”地展示了分解方式与问题的“几何”或“组合”属性之间的内在联系. 具体地讲,就是如何控制分解所派生的不同几何体之间的重叠(球、tube、tile、长方体与曲线等),曲面的“曲率”与“横截”等性质在建立控制估计中起着关键作用. 本次报告中,苗老师从一些著名算子出发, 不仅在物理空间中研究函数与算子, 同时在频率空间中研究它们之间的相互作用, 着力讨论了诸如Hormander-Mikhlin乘子定理、Coifman-Meyer乘子定理、T(1)定理、Schur-Test、Christ-Kiselev引理及众多著名不等式在其中发挥的作用。报告过程中,苗老师介绍了很多公开问题,鼓励年轻人探索数学前沿问题。报告内容非常丰富,层次分明,讲解特别生动形象,深入浅出。参会老师就报告内容进行了热烈的讨论交流。
报告人简介: 苗长兴, 曾荣获国家级青年基金、于敏数理科学奖、中国工程物理研究院杰出专家、中国工程物理研究院科技创新一等奖,是我国自己培养的在国际偏微分方程和调和分析领域有重要影响的杰出数学家。近年来在国际一流的学术刊物(如:CPAM、CMP、ARMA、MZ、JFA、JMPA、SIAM、AIHP、CPDE、PLMS等)上发表论文百余篇, 主要贡献表现在调和分析、非线性色散方程的散射理论与流体动力学方程的数学理论等研究领域,解决了若干个具有国际影响的数学问题,得到了著名数学家Kenig、 Constantin等国际同行的高度评价。
